In alternating current (AC) circuits the electric power consumption is not only measured in watts [W], there are 3 other components that must considered: real power P [W], reactive power Q [VAr] and apparent power S [VA].

Without deepening into electrical circuit theories, formulas or phasors, I will try to clarify these concepts and their relation to power factor.
VA means Volt-Amps, the product of Volts x Amps, which is commonly known as watts (measure of electric power). In AC systems VA is technically used for the apparent power S, whereas watts measures real power P.
Therefore in an AC lighting system, P can be defined as the real power required to run a luminaire, whereas S is the (apparent) electric power that needs to be supplied to the luminaire. But, isn’t it the same, P = S? Not always. In AC circuits the relationship between S and P is given by the power triangle:

In resistive circuits, where the loads are pure resistors without any reactive component, S = P because Q = 0, and the power triangle becomes in a straight line with the angle θ = 0. This is the case of incandescent lights where the tungsten filaments are simple resistors.
But most of the lighting systems available in the market nowadays are LED electronic systems, fluorescent lamps, high intensity discharge lamps, and they require control gear to run the lamps/light sources. The presence of ballasts, transformers and electronic drivers in the circuits include reactive components (inductors and capacitors), which make the reactive power Q ≠ 0 and so, S > P (see Figure 1).
In these cases, where S ≠ P, the relation between S and P is established by the power factor of the circuit. Power factor (PF and sometimes λ) is a number between 0 and 1, represented in the power triangle as the cosine of the angle θ (cos θ). It is a measure of how effectively electrical power is being used in our lighting installation.
PF = cos θ [0... 1] P = S x PF
In lighting circuits with reactive equipment, power factor is an important parameter to be considered. A PF < 1 means that the current shall be increased to supply the same level of real power P to the light source; and the lower the PF, the higher the current necessary to perform the same job. On the other hand, the closer the PF to unity (1), the less current is necessary, making our lighting circuit more efficient. That is why Q is considered the inefficient component of electric power.
What are the consequences of not taking into account the power factor?
The effects of a low PF are manifested in a high power consumption of our lighting installation and eventually in the cost of the electricity bill; especially if the demand tariff is calculated on a kilo-volt ampere [kVA] basis.
Also the components of the circuit, including the wires may suffer overheating after long periods of operation due to the increase of electric current circulation. This case may not be a big problem in small or residential installations, but an excessive heat generated could damage the equipment of bigger lighting systems incurring in additional maintenance costs.
The light output of the luminaires can be also compromised due to undesired light dimming.
Thus, the desired performance of any lighting installation (and electrical circuit in the end) is to maximize the real power P while reducing to the minimum the reactive power Q.
And how can I obtain a high power factor?
A lighting system with a low PF can be corrected in order to reduce the reactive component of the power (Q) and take the power factor closer to 1.
As mentioned before, reactive power Q is due to the presence of 2 types of components in the electrical circuit: inductive loads (inductors, transformers or coils) and capacitive loads (capacitors). However, inductive and capacitive loads compensate each other so a circuit with a balance of inductive and capacitive components will result in a diminished reactive power Q.
As an example: let’s consider we want to install a 600W lighting system, by means of 4 floodlights of 150W with HID metal halide lamps. The electrical contractor, during the installation did not take into account the power factor of the circuit, so to run the 600W installation it is required to supply 920VA.
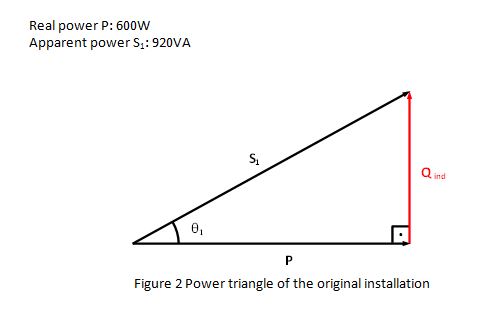
Then, the power factor of the electrical installation is: PF = P/S1 = 600/920 = 0.65
PF = 0.65 = cos θ1 θ1 = 49.5˚ (see Figure 2)
Being a right-angled triangle we can apply the Pythagorean theorem: Qind2 = S12 - P2 = 9202 - 6002
Qind = 697.5 VAr
The 4 HID luminaires run with electromagnetic ballasts, which are highly inductive components inside the circuit, increasing the reactive power Q of the installation (called Qind due to the inductors).
After several months in operation, the electrical contractor realises that indeed the power factor of the lighting installation is not very high, as a result of the reactive components not being correctly balanced. In order to counteract the inductive load and reduce the reactive power Qind the electrical contractor calculates and installs in the circuit the adequate capacitive components (capacitors) which provide an opposite reactive power: Qcap.
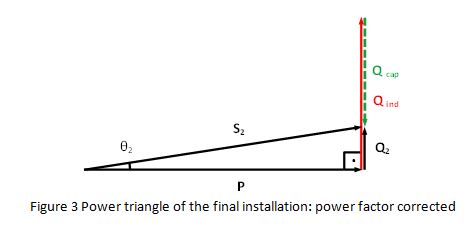
The result of Qind - Qcap is a new value of reactive power Q2 much smaller than the original Q1, which brings the apparent power S2 closer to the real power P. When measuring again the power S2 consumed by the lighting installation, the value obtained is 660 VA:
Real power P: 600 W
Apparent power S2: 660 VA
Power factor of the installation, PF: PF = P/S2 = 600/660 = 0.91
PF = 0.91 = cos θ2 θ2 = cos-1 0.91 = 24.5˚
Q2 = Qind - Qcap Q22 = S22 - P2 = 6602 - 6002 Q2 = 275.0 VAr
The difference between the original power S1 of 920 VA and the final S2 660 VA is 260 VA, a value that in our annual electricity tariff could represent a big saving.
Conclusions
Power factor is indeed a key parameter in any lighting system running on mains AC supply. The higher the wattage of our luminaires, the higher the power they require to operate, and bigger is the impact of the power factor on the electricity consumption.
The control gear and equipment of any luminaire shall always provide information about the power factor, in order to identify the performance and energy consumption of our lighting systems, and correct it if necessary.
Some Australian Standards, such as AS/NZS 1158.6 specify a minimum value of nominal power factor required for the operation of the luminaires, of no less than 0.85.
Customer should always contact a qualified electrician to get professional advice and to carry out this type of installation and jobs.
